financialvorti.blogg.se - Backpropagation of cnn fromscratch

#BACKPROPAGATION OF CNN FROMSCRATCH PLUS#

In the classical backpropagation algorithm, the weights are changed according to the gradient descent direction of an error surface. Learning will be achieved by adjusting the weights such that is as close as possible or equals to corresponding.

#BACKPROPAGATION OF CNN FROMSCRATCH PLUS#

is the convolved input vector at layer plus the bias represented as.

is the weight matrix connecting neurons of layer with neurons of layer.

Filter or kernel is of dimension has by as the iterators.

Input is of dimension and has by as the iterators.

is the layer where is the first layer and is the last layer.

To help us explore the forward and backpropagation, we shall make use of the following notation: The convolution operation carried out here is the same as cross-correlation, except that the kernel is “flipped” (horizontally and vertically).įor the purposes of simplicity we shall use the case where the input image is grayscale i.e single channel. The output from this convolution procedure is as follows: Subsequently for a bank of filters we have and biases, one for each filter. In the case of images, we could have as input an image with height, width and channels (red, blue and green) such that.

Convolution Neural Networks - CNNsĬNNs consists of convolutional layers which are characterized by an input map, a bank of filters and biases.

it is easy to see that convolution is the same as cross-correlation with a flipped kernel i.e: for a kernel where. Given an input image and a filter (kernel) of dimensions, the convolution operation is given by:įrom Eq. Given an input image and a filter (kernel) of dimensions, the cross-correlation operation is given by: Convolution The last layer of this fully-connected MLP seen as the output, is a loss layer which is used to specify how the network training penalizes the deviation between the predicted and true labels.īefore we begin lets take look at the mathematical definitions of convolution and cross-correlation: Cross-correlation After several convolutional and pooling layers, the image size (feature map size) is reduced and more complex features are extracted.Įventually with a small enough feature map, the contents are squashed into a one dimension vector and fed into a fully-connected MLP for processing. This is then followed by a pooling operation which as a form of non-linear down-sampling, progressively reduces the spatial size of the representation thus reducing the amount of computation and parameters in the network.Įxisting between the convolution and the pooling layer is an activation function such as the ReLu layer a non-saturating activation is applied element-wise, i.e. Utilizing the weights sharing strategy, neurons are able to perform convolutions on the data with the convolution filter being formed by the weights. This sharing of weights ends up reducing the overall number of trainable weights hence introducing sparsity. Neurons in CNNs share weights unlike in MLPs where each neuron has a separate weight vector.

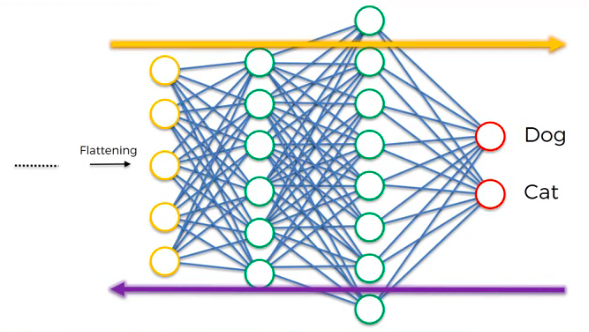
Backpropagation In Convolutional Neural Networks Jefkine, 5 September 2016 IntroductionĬonvolutional neural networks (CNNs) are a biologically-inspired variation of the multilayer perceptrons (MLPs).